Designing A Learning System in Machine Learning
Designing a Learning System
In order to get a successful learning system, it should be designed for a proper design, several steps should be followed.
Why we need to follow steps because in order to get perfect and efficient system.
Steps:
- Choosing a training example
-
Choosing the target Example
-
Choosing a representation for target function
-
Choosing a learning algorithm for approximating the target function
1. Choosing the Training Experience
Choosing a training experience contain three attribute are taken
• Type of feedback
• Degree
• Distribution of example
Type of feedback
Weather the training experience provides direct or indirect feedback regarding the choices made by Performance system.
Direct feedback
Indirect feedback
Example : checkers game
Degree
Of which learners (person who undergoing training) will control the sequence of training.
Example
Distribution Of Example
How well it respond the distribution of example aver which Performance of final system is measured more possible combinations, situation.
Example: testing job
2. Choosing a Target Function
First we need to chose the target experience, what type of knowledge is leaner and how it is used by the performance system
Example: checkers game
It contains the legal moves from any board, the program how to choose the best moves among them legal moves
- Travel only in the forward direction
-
At a time you can move only once in a chance
-
In a diagonal direction
-
Jumping over the opponent side
-
Back moves are not allowed ( only legal moves)
One move i.e., is called target move
Target Function – V(b)
Board state = b
Legal moves set = B
How do you assign the Value of b
b Is the final board state that is won, then V(b)=100
b Is the final board state that is lost, then V(b)=-100
b Is the final board state that is draw, then V(b)=0
If b is not a final state then V(b)=〖V(b)〗^’
b^’- Is the best final state
Choosing a Representation of Target Function
For any board state (b), we calculate function ‘c’ as a linear combination ( the degree is 1 ), of following board features
I.e. c (b)
Features
x_1= Number of black pieces on board
x_2= Number of red pieces on board
x_3= Number of black king pieces on board
x_4= Number of red king pieces on board
x_5= Number of black pieces threatened by red, the black which can beaten by red
x_6= The number of red pieces threatened by black
Linea function representation in the form of
V(b)=w_(0x_1 )+w_1 x_1+w_2 x_2+w_3 x_3+w_4 x_4+w_5 x_5+w_6 x_6
x_1—–x_6= These are feature
w_1—–w_6=Numerical weights for each and every features
w_0=Called additive constant to the board value
Choosing a learning for approximating the target function
Here we are learning an algorithm for approximate the target function
In order to understand a target function we need to set some of the training example
The training example it will describe a particular board state and the training value
Board state is represented by b
Training value is represented by V_train (b)
Training Example is represented in the form of
Training Example is required in order to understand clearly about the target function
order pair=(b,V_train (b))
b-x=coordinate
V_train (b)=y-coordinate
Example: the number of black coins to win the game x_2=0
x_2 Means the number of red coins
V_train (b)=+100
b=(x_1=3,x_2=0,x_3=1,x_4=0,x_5=0,x_6=0)
<(x_1=3,x_2=0,x_3=1,x_4=0,x_5=0,x_6=0)+100>
We need to do 2 steps in this phase
Estimating the Training Value
In each and every steps we need to estimate, in every step we need to consider the successor, depending upon the next step of the opponents, assign a value to successor it represents the next board state.
V_train (b)=V^n (successor( b))
It will estimate that this move will help or destroy opponents
V^n-It represents approximation
Adjusting the Weights
We will be using some algorithms to find Weights linear function. Here we are using LSM ( Least Mean Square) it is used to maximize the error
Error=(V_train (b)-V^n 〖 (b)〗^n 2=Positive
If error = 0 we need to change weight
If error is positive each weight is increased is proportion
If error is negative each weight is decreased is proportion
Final design
In the final design we have four different modules
Performance system
Critic
Generalizer
Experiment Generator
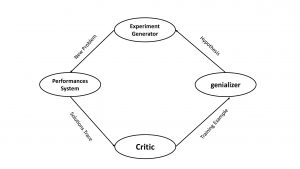
Any new problem taken as input , output will be solution trace ( grace history) this kind of problem is that previously, what happened that will be output for the Performance system.
It will take input as the previous history by the performance system generator an output regarding the training example.
Generalizer it will take input as a training example, it will generate a hypothesis ( is nothing but an imagination) ,
experimental generator it will take input as a hypothesis, it will generate the input, it will generate a new problem.
It will maximize the experiment Generator.